排序算法

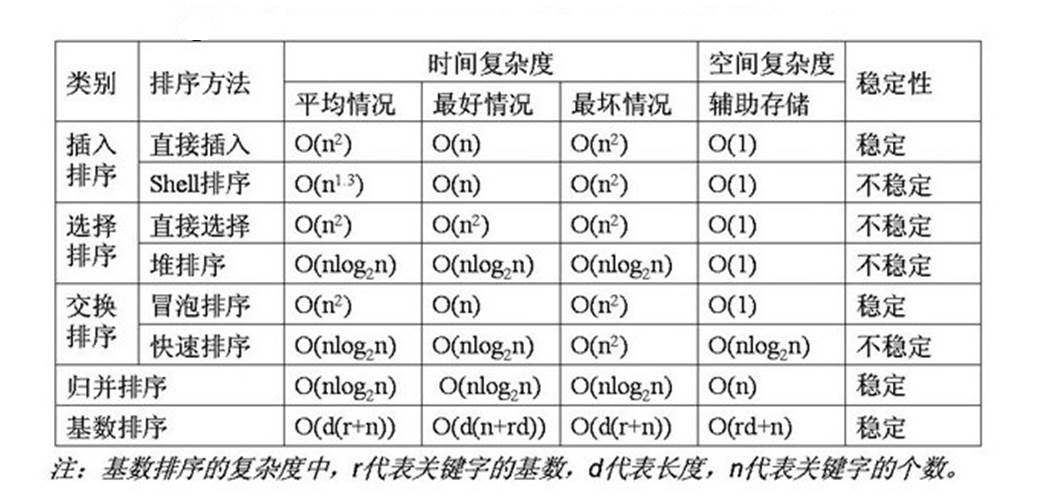
各类排序算法时间复杂度和空间复杂度对照表

Image text

一、冒泡排序（Bubble Sort）

基本思路：

依次比较相邻的两个数，将小数放在前面，大数放在后面。即在第一趟：首先比较第1 个和第 2 个数，将小数放前，大数放后。然后比较第 2 个数和第 3个数，将小数放前，大数放后，如此继续，直至比较最后两个数，将小数放前，大数放后。至此第一趟结束，将最大的数放到了最后。在第二趟：仍从第一对数开始比较（因为可能由于第2 个数和第 3 个数的交换，使得第 1 个数不再小于第 2个数），将小数放前，大数放后，一直比较到倒数第二个数（倒数第一的位置上已经是最大的），第二趟结束，在倒数第二的位置上得到一个新的最大数（其实在整个数列中是第二大的数）。如此下去，重复以上过程，直至最终完成排序。

C++示例

#include <algorithm>
#include <iostream>

template <class Container>
void bubble_sort(Container& data, int size)
{
    for (int i = 0; i < size; ++i) {
        for (int j = 1; j < size - i; ++j) {
            if (data[j - 1] > data[j]) {
                std::swap(data[j], data[j - 1]);
            }
        }
    }
}

template <class Container>
void bubble_sort_ex(Container& data, int size)
{
    bool has_changed = true;
    do {
        has_changed = false;
        for (int i = 1; i < size; ++i) {
            if (data[i] < data[i - 1]) {
                std::swap(data[i], data[i - 1]);
                has_changed = true;
            }
        }
        --size;
    } while (has_changed);
}

int main(int argc, char** argv)
{
    {
        int data[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
        int length = int(sizeof(data) / sizeof(*data));
        bubble_sort(data, length);
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    {
        double data[] = { 3.3, 5.5, 3.2, 0.2, 8.1, 6.1, 1.2, 5.4, 8.7, 6.3, 2.2, 4.4, 9.7, 9.5, 7.7, 4.3, 0.1, 2.8, 6.6 };
        int length = int(sizeof(data) / sizeof(*data));
        bubble_sort(data, length);
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    {
        int data[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
        int length = int(sizeof(data) / sizeof(*data));
        bubble_sort_ex(data, length);
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    {
        double data[] = { 3.3, 5.5, 3.2, 0.2, 8.1, 6.1, 1.2, 5.4, 8.7, 6.3, 2.2, 4.4, 9.7, 9.5, 7.7, 4.3, 0.1, 2.8, 6.6 };
        int length = int(sizeof(data) / sizeof(*data));
        bubble_sort_ex(data, length);
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    system("pause");
}

二、选择排序（Selection sort）

基本思路：

每一趟从待排序的数据元素中选出最小（或最大）的一个元素，顺序放在已排好序的数列的最后，直到全部待排序的数据元素排完。

C++示例

#include <algorithm>
#include <iostream>

template <class Container>
void select_sort(Container& data, int size)
{
    for (int i = 0; i < size - 1; ++i) {
        int min = i;
        for (int j = i + 1; j < size; ++j) {
            if (data[j] < data[min]) {
                min = j;
            }
        }
        if (i != min) {
            std::swap(data[i], data[min]);
        }
    }
}

int main(int argc, char** argv)
{
    {
        int data[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
        int length = int(sizeof(data) / sizeof(*data));
        select_sort(data, length);
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    {
        double data[] = { 3.3, 5.5, 3.2, 0.2, 8.1, 6.1, 1.2, 5.4, 8.7, 6.3, 2.2, 4.4, 9.7, 9.5, 7.7, 4.3, 0.1, 2.8, 6.6 };
        int length = int(sizeof(data) / sizeof(*data));
        select_sort(data, length);
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    system("pause");
}

三、快速排序（Quicksort）

基本思路：

设要排序的数组是 A[0]……A[N-1]，首先任意选取一个数据（通常选用第一个数据）作为关键数据，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，这个过程称为快速排序。

一趟快速排序的算法是：
1. 设置两个索引 I、J，排序开始的时候：I = 0，J = N - 1；
2. 以第一个数组元素作为关键数据，赋值给 key，即 key = A[0]；
3. 从 J 开始向前搜索，即由后开始向前搜索（J = J - 1），找到第一个小于 key 的值 A[J]，并与 A[I]交换；
4. 从 I 开始向后搜索，即由前开始向后搜索（I = I + 1），找到第一个大于 key 的 A[I]，与 A[J]交换；
5. 重复第3、4、5步，直到 I = J；

C++示例

#include <algorithm>
#include <iostream>

template <class Container>
void quick_sort(Container& data, int low, int high)
{
    if (low >= high)
        return;

    auto key = data[low];
    int i = low;
    int j = high;
    while (i < j) {
        while (i < j && data[j] >= key)
            j--;
        if (data[j] < key)
            data[i++] = data[j]; // 比 key 小的移到前端
        while (i < j && data[i] <= key)
            i++;
        if (data[i] > key)
            data[j--] = data[i]; // 比 key 大的移到后端
    }
    data[i] = key;
    quick_sort(data, low, i - 1);
    quick_sort(data, i + 1, high);

}

int main(int argc, char** argv)
{
    {
        int data[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
        int length = int(sizeof(data) / sizeof(*data));
        quick_sort(data, 0, length - 1); // 下标最大值, 而不是数组长度
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    {
        double data[] = { 3.3, 5.5, 3.2, 0.2, 8.1, 6.1, 1.2, 5.4, 8.7, 6.3, 2.2, 4.4, 9.7, 9.5, 7.7, 4.3, 0.1, 2.8, 6.6 };
        int length = int(sizeof(data) / sizeof(*data));
        quick_sort(data, 0, length - 1); // 下标最大值, 而不是数组长度
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    system("pause");
}

四、插入排序（Insertion sort）

基本思路：

将第一个元素看成是一个有序的子序列，在依次从第二个记录起依次插入到这个有序的子序列中。

C++示例

#include <algorithm>
#include <iostream>

template <class Container>
void insert_sort(Container& data, int size)
{
    for (int i = 1; i < size; ++i) {
        auto temp = data[i];
        int j = i - 1;
        for (; j >= 0; j--) { //内循环负责找到应该插入的下标
            if (num >= data[j])
                break;
            data[j + 1] = data[j];
        }
        data[j + 1] = temp;
    }
}

int main(int argc, char** argv)
{
    {
        int data[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
        int length = int(sizeof(data) / sizeof(*data));
        insert_sort(data, length);
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    {
        double data[] = { 3.3, 5.5, 3.2, 0.2, 8.1, 6.1, 1.2, 5.4, 8.7, 6.3, 2.2, 4.4, 9.7, 9.5, 7.7, 4.3, 0.1, 2.8, 6.6 };
        int length = int(sizeof(data) / sizeof(*data));
        insert_sort(data, length);
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    system("pause");
}

五、希尔排序（Shell’s Sort）

基本思路：

先取一个小于 n 的整数 d1 作为第一个增量，把文件的全部记录分成 d1个组。所有距离为 dl 的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量 d2<d1 重复上述的分组和排序，直至所取的增量 dt=1(dt<dt-l<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。

C++示例

#include <algorithm>
#include <iostream>

template <class Container>
void shell_sort(Container& data, int size)
{
    int gre = size / 2;
    while (gre) {
        for (int i = gre; i < size; ++i) {
            auto temp = data[i];
            int j = i;
            while (j >= gre && temp < data[j - gre]) {
                data[j] = data[j - gre];
                j = j - gre;
            }
            data[j] = temp;
        }
        gre = gre / 2;
    }
}

int main(int argc, char** argv)
{
    {
        int data[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
        int length = int(sizeof(data) / sizeof(*data));
        shell_sort(data, length);
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    {
        double data[] = { 3.3, 5.5, 3.2, 0.2, 8.1, 6.1, 1.2, 5.4, 8.7, 6.3, 2.2, 4.4, 9.7, 9.5, 7.7, 4.3, 0.1, 2.8, 6.6 };
        int length = int(sizeof(data) / sizeof(*data));
        shell_sort(data, length);
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    system("pause");
}

六、归并排序（Merge sort）

基本思路：

归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

C++示例

#include <algorithm>
#include <iostream>
#include <vector>

template <class CType, class Container>
void merge_sort(Container& data, int low, int mid, int high)
{
    std::vector<CType> p(high + 1);
    int i = low;
    int j = low;
    int h = mid + 1;
    while (h <= high && j <= mid) {
        if (data[j] <= data[h]) {
            p[i++] = data[j++];
        } else {
            p[i++] = data[h++];
        }
    }
    while (j <= mid) {
        p[i++] = data[j++];
    }
    while (h <= high) {
        p[i++] = data[h++];
    }
    for (i = low; i <= high; i++) {
        data[i] = p[i];
    }
}

template <class CType, class Container>
void merge(Container& data, int low, int high)
{
    if (low >= high)
        return;

    int mid = (low + high) / 2;
    merge<CType>(data, low, mid);
    merge<CType>(data, mid + 1, high);
    merge_sort<CType>(data, low, mid, high);
}

int main(int argc, char** argv)
{
    {
        int data[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
        int length = int(sizeof(data) / sizeof(*data));
        merge<int>(data, 0, length - 1); // 下标最大值, 而不是数组长度
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    {
        double data[] = { 3.3, 5.5, 3.2, 0.2, 8.1, 6.1, 1.2, 5.4, 8.7, 6.3, 2.2, 4.4, 9.7, 9.5, 7.7, 4.3, 0.1, 2.8, 6.6 };
        int length = int(sizeof(data) / sizeof(*data));
        merge<double>(data, 0, length - 1); // 下标最大值, 而不是数组长度
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    system("pause");
}

七、堆排序（Heapsort）

基本思路：

小根堆：所有子节点都大于其父节点；

大根堆：所有子节点都小于其父节点；

大根堆的基本思路：
1. 先初始化 A[1…..n]建成一个大根堆，此根为初始化的无序区。
2. 再将关键字最大的记录 A[1]（堆顶）和无序区的最后一个记录 A[n]交换，由此得到新的无序区 A[n-1]和有序区 A[n]且满足 A[1…..(n-1)]<=A[n];
3. 将余下的数据调整为堆，然后重复（2）的过程
4. 对调整的堆重复上面的过程，直到无序区只有一个元素为止。

C++示例

#include <algorithm>
#include <iostream>

template <class Container>
void heap_adjust(Container& data, int i, int length)
{
    int son = i * 2 + 1;
    while (son < length) {
        if (son + 1 < length && data[son] < data[son + 1])
            son++;
        if (data[i] > data[son])
            return;

        std::swap(data[i], data[son]);
        i = son;
        son = i * 2 + 1;
    }
}

template <class Container>
void heap_sort(Container& data, int length)
{
    // 将 heap[0, Lenght-1] 建成大根堆
    for (int i = length / 2 - 1; i >= 0; i--) {
        heap_adjust(data, i, length);
    }
    for (int i = length - 1; i > 0; i--) {
        std::swap(data[0], data[i]);  // 与最后一个记录交换
        // 将 heap[0..i]重新调整为大根堆
        heap_adjust(data, 0, i);
    }
}

int main(int argc, char** argv)
{
    {
        int data[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
        int length = int(sizeof(data) / sizeof(*data));
        heap_sort(data, length);
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    {
        double data[] = { 3.3, 5.5, 3.2, 0.2, 8.1, 6.1, 1.2, 5.4, 8.7, 6.3, 2.2, 4.4, 9.7, 9.5, 7.7, 4.3, 0.1, 2.8, 6.6 };
        int length = int(sizeof(data) / sizeof(*data));
        heap_sort(data, length);
        for (int i = 0; i < length; i++)
            std::cout << data[i] << ' ';
        std::cout << std::endl;
    }
    system("pause");
}